ระบบพิกัดเชิงขั้ว
ระบบพิกัดเชิงขั้วในระนาบประกอบด้วย
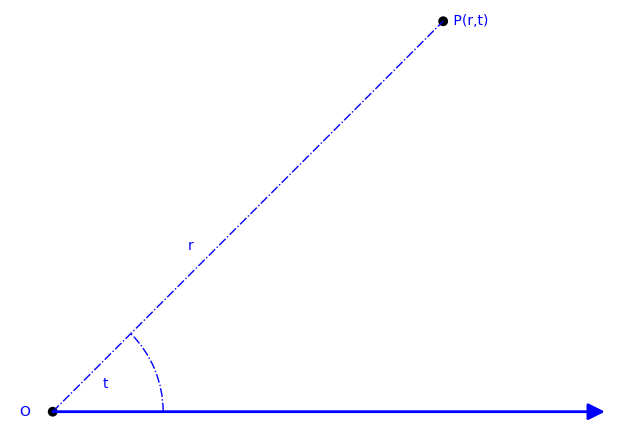
จุดคงที่ $O$เรียกว่า จุดกำเนิด หรือ จุดขั้ว
และรังสีไปทางขวาของจุดกำเนิด เรียกว่า แกนเชิงขั้ว
ในระบบพิกัดเชิงขั้ว จุด $P$ กำหนดโดย $P(r,t)$ โดยที่ $r$ เป็นระยะจากจุด $O$ ถึง จุด $P$
และ $ t $ เป็นมุมที่วัดจากแกนเชิงขั้วถึง เส้นตรง $OP$ ดังรูป
เครื่องหมายของ $r$ และ $t$ เป็นได้ทั้ง ศูนย์ บวกและลบ มีเงื่อนไขดังต่อไปนี้
- $r=0$
แทน จุดขั้ว $O$
- $r>0$
แทน จุดที่วัดระยะห่างจากจุดขั้วเป็นระยะทาง $r$ หน่วย แขน $OP$ทำมุม $t$ กับแกนเชิงขั้ว
- $r<0$
แทน จุดที่วัดระยะห่างจากจุดขั้วเป็นระยะทาง $\mid r \mid $ หน่วย แขน $OP$ทำมุม $t+ \pi$ กับแกนเชิงขั้ว
- $t=0$
แทนจุด ที่อยู่บนแกนเชิงขั้วทางขวา (เมื่อ $r>0$)และอยู่บนแกนเชิงขั้วทางซ้าย (เมื่อ $r<0$)
- $t>0$
แทนจุด ที่วัดจากแกนเชิงขั้วในทิศทวนเข็มนาฬิกาห่างจากจุดขั้วระยะทาง$\mid r \mid $ หน่วย
- $t<0$
แทนจุด ที่วัดจากแกนเชิงขั้วในทิศตามเข็มนาฬิกาห่างจากจุดขั้วระยะทาง$\mid r \mid $ หน่วย
ตัวอย่าง
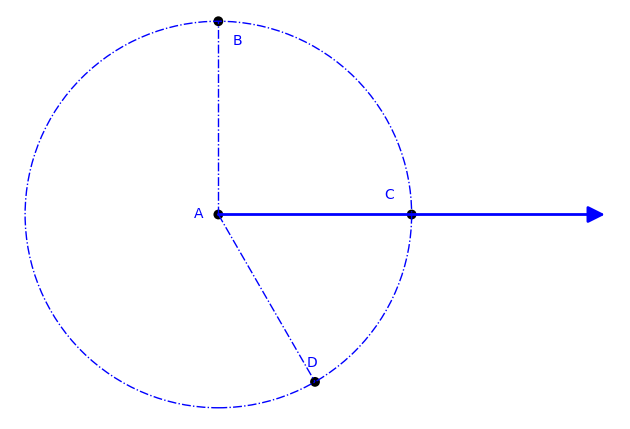
จงลงจุด $A(0,\frac{\pi}{4}),B(1,\frac{\pi}{2}) ,C(-1,\pi) ,D(1,-\frac{\pi}{3}) $ในระบบพิกัดเชิงขั้ว
ความสัมพันธ์ระหว่างระบบพิกัดเชิงขั้วกับระบบพิกัดฉาก
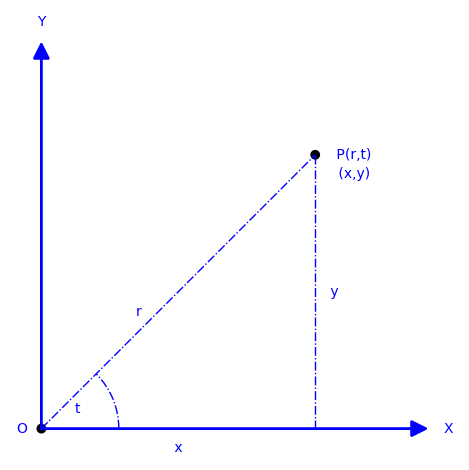
ให้ จุดขั้ว $O$ ในพิกัดเชิงขั้ว เป็นจุด $(0,0)$ ในพิกัดฉาก
และ แกนขั้ว ในพิกัดเชิงขั้ว คือ แกน $x$ ทางด้านบวกในพิกัดฉาก
ดังนั้น จุด ในระนาบ เราจะได้ความสัมพันธ์ ระหว่างพิกัดเชิงขั้ว กับ พิกัดฉาก ดังนี้
สมมติจุด ในระบบพิกัดเชิงขั้วคือ $(r,t)$ แต่ในระบบพิกัดฉากเป็น $(x,y)$ ดังรูป
จะได้ว่า
$ x= rcos(t) , y =rsin(t) $
และ $ r^{2}=x^{2}+y^{2} , tan(t) = \frac{y}{x} $ เมื่อ $x\neq 0 $
ตัวอย่าง
จงแปลงจุด $(1,\frac{\pi}{3}) $ ในพิกัดเชิงขั้ว เป็นพิกัดฉาก
วิธีทำ
จาก $ x= rcos(t) = 1cos(\frac{\pi}{3})=\frac{1}{2}$
และ $ y = rsin(t) = 1sin(\frac{\pi}{3})=\frac{\sqrt{3}}{2}$
ดังนั้น จุด $(1,\frac{\pi}{3}) $ ในพิกัดเชิงขั้ว คือ จุด $(\frac{1}{2},\frac{\sqrt{3}}{2}) $ ในพิกัดฉาก
ตัวอย่าง
จงแปลงจุด $(2,2) $ ในพิกัดฉาก เป็นพิกัดเชิงขั้ว
วิธีทำ
จาก $ r^{2}=x^{2}+y^{2} =2^{2}+2^{2}= 8 $
ดังนั้น $ r = \pm \sqrt{8}=\pm 2\sqrt{2} $
และ $tan(t) = \frac{y}{x} =\frac{2}{2}= 1 $
นั่นคือ $t= \frac{\pi}{4} ,\frac{5\pi}{4},...$
ดังนั้น จุด $(2,2) $ ในพิกัดฉาก คือจุด $ (2\sqrt{2},\frac{\pi}{4}) $ ในพิกัดเชิงขั้ว
ข้อสังเกต
จุด $(2,2) $ ในพิกัดฉาก อาจเป็น จุด $ (-2\sqrt{2},\frac{5\pi}{4}) $ในพิกัดเชิงขั้ว
หรือ อาจเป็น จุด $ (-2\sqrt{2},-\frac{3\pi}{4}) $
แต่ในที่นี้เรามักสนใจกรณีที่ $ r > 0 $
ตัวอย่าง
จงแปลงสมการพิกัดฉากต่อไปนี้
- $x^{2}+y^{2} = 1 $
- $x^{2}+2x+y^{2} = 0 $
- $x^{2}-2y+y^{2} = 0 $
เป็นสมการในพิกัดเชิงขั้ว
วิธีทำ
- จาก $ r^{2} = x^{2}+y^{2} = 1 $
ดังนั้น $ r = \pm 1 $ หรือ $ r = 1 $
- $0=x^{2}+2x+y^{2} = r^{2}+2rcos(t)=r(r+2cos(t)) $
นัั่นคือ $r=0$ หรือ $r+2cos(t)=0$
แต่จาก $r=0$ คือสมการที่มีกราฟคือจุดขั้วจุดเดียว
และ เมื่อ $t=\frac{\pi}{2}$ แทนในสมการ $r+2cos(t)=0$ จะได้ $r =0$
ดังนั้น สมการ$x^{2}+2x+y^{2} = 0 $ เขียนเป็นสมการเชิงขั้วได้ $r+2cos(t)=0$ หรือ $r=-2cos(t)$
- $0=x^{2}-2y+y^{2} = r^{2}-2rsin(t)=r(r-2sin(t)) $
นัั่นคือ $r=0$ หรือ $r-2sin(t)=0$
แต่จาก $r=0$ คือสมการที่มีกราฟคือจุดขั้วจุดเดียว
และ เมื่อ $t=0$ แทนในสมการ $r-2sin(t)=0$ จะได้ $r =0$
ดังนั้น สมการ$x^{2}-2y+y^{2} = 0 $ เขียนเป็นสมการเชิงขั้วได้ $r-2sin(t)=0$ หรือ $r=2sin(t)$
ตัวอย่าง
จงแปลงสมการพิกัดเชิงขั้วต่อไปนี้
- $r = 9cos(t) $
- $r = -16sin(t) $
- $r = 1+sin(t) $
เป็นสมการในพิกัดฉาก
วิธีทำ
- นำ $r$ คูณสมการได้ $ r^{2} = 9rcos(t) $
หรือ $ x^{2}+y^{2} = 9x $ หรือ $ x^{2}-9x+y^{2} = 0 $
- นำ $r$ คูณสมการได้ $r^{2}=-16rsin(t) $
หรือ $ x^{2}+y^{2} = -16y$ หรือ $ x^{2}+y^{2} +16y = 0$
- นำ $r$ คูณสมการได้ $r^{2}=r+rsin(t) $
หรือ $x^{2}+y^{2} = \sqrt{x^{2}+y^{2}} + y $
การเขียนกราฟในระบบพิกัดเชิงขั้ว
การเขียนกราฟในระบบพิกัดเชิงขั้วที่มีสมการแสดงความสัมพันธ์ $r=f(t) $ หรือ $F(r,t)=0$
เรามักพิจารณาหาค่า $t$ ที่ทำให้ $r=0$ เพื่อจะได้รู้ว่า กราฟผ่านจุดขั้วหรือไม่ จากนั้นก็อาจจะวิเคราะห์พิจารณาที่ $t=0,\frac{\pi}{2},\pi,\frac{3\pi}{2}, ... $
เพื่อดูว่ากราฟผ่านจุดใดบ้าง
จากนั้นอาจพิจารณาการสมมาตรของกราฟว่ากราฟนี้สมมาตรกับอะไรบ้างซึ่งในการพิจารณาการสมมาตรนั้นเราอาจพิจาณาได้ดังนี้
- สมมาตรกับแกนเชิงขั้ว
ทดสอบโดย
- แทน $t$ด้วย$-t$
แล้วตรวจสอบดูว่าสมการที่ได้ยังเหมือนเดิมหรือไม่ ถ้าได้สมการเดิมก็แสดงว่าสมมาตรกับแกนขั้วแต่สมการแตกต่างจากเดิมอาจจะต้องทดสอบต่อโดย
- แทน $t$ด้วย$\pi-t$ และ แทน $r$ด้วย$-r$
แล้วตรวจสอบดูว่าสมการที่ได้ยังเหมือนเดิมหรือไม่ ถ้าได้สมการเดิมก็แสดงว่าสมมาตรกับแกนขั้วแต่สมการแตกต่างจากเดิม ก็สรุปว่า ไม่สมมาตรกับแกนขั้ว
- สมมาตรกับเส้นตรง $t=\frac{\pi}{2}$
- แทน $t$ด้วย$\pi-t$
แล้วตรวจสอบดูว่าสมการที่ได้ยังเหมือนเดิมหรือไม่ ถ้าได้สมการเดิมก็แสดงว่าสมมาตรกับ เส้นตรง $t=\frac{\pi}{2}$ แต่สมการแตกต่างจากเดิมอาจจะต้องทดสอบต่อโดย
- แทน $t$ด้วย$-t$ และ แทน $r$ด้วย$-r$
แล้วตรวจสอบดูว่าสมการที่ได้ยังเหมือนเดิมหรือไม่ ถ้าได้สมการเดิมก็แสดงว่าสมมาตร กับ เส้นตรง $t=\frac{\pi}{2}$ แต่ถ้าสมการแตกต่างจากเดิม ก็สรุปว่า ไม่สมมาตรกับ เส้นตรง $t=\frac{\pi}{2}$
- สมมาตรกับจุดขั้ว
- แทน $t$ด้วย$\pi + t$
แล้วตรวจสอบดูว่าสมการที่ได้ยังเหมือนเดิมหรือไม่ ถ้าได้สมการเดิมก็แสดงว่าสมมาตรกับจุดขั้วแต่สมการแตกต่างจากเดิมอาจจะต้องทดสอบต่อโดย
- แทน $r$ด้วย$-r$
แล้วตรวจสอบดูว่าสมการที่ได้ยังเหมือนเดิมหรือไม่ ถ้าได้สมการเดิมก็แสดงว่าสมมาตรกับจุดขั้วแต่สมการแตกต่างจากเดิม ก็สรุปว่า ไม่สมมาตรกับจุดขั้ว
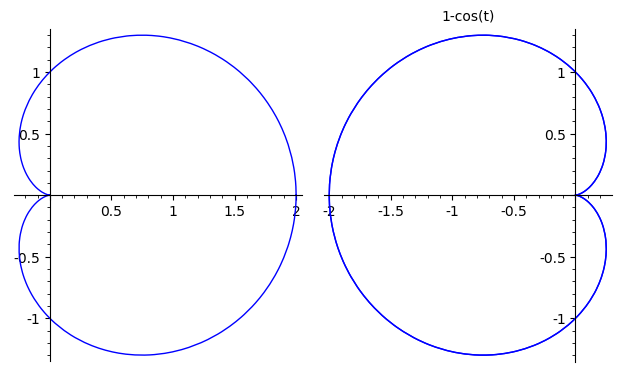
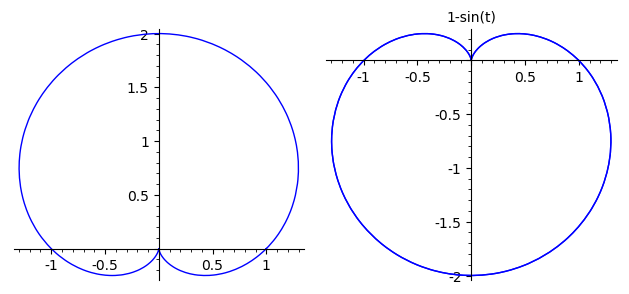
เส้นโค้งรูปหัวใจ หรือ คาร์ดิออยด์
มีสมการทั่วไปคือ
- $r=a(1+cos(t))$
- $r=a(1-cos(t))$
- $r=a(1+sin(t))$
- $r=a(1-sin(t))$
เมื่อ $a>0 $
กรณี $a=1$ มีกราฟดังนี้
เส้นโค้งลีมาซอง
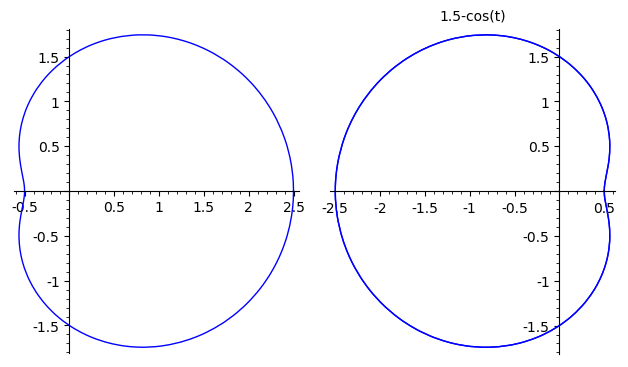
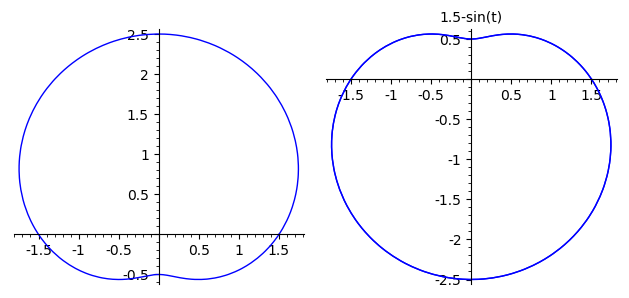
สมการทั่วไปคือ
- $r=a+bcos(t)$
- $r=a-bcos(t)$
- $r=a+bsin(t)$
- $r=a-bsin(t)$
เมื่อ $a,b >0 $ และ $a \ne b $
กรณี $ 0 < b < a < 2b $ จะได้กราฟของเส้นโค้งลีมาซอง เป็นแบบคล้ายแอปเปิล มีรอยบุ๋ม ดังนี้
เมื่อ $a=1.5, b=1 $ มีกราฟดังนี้
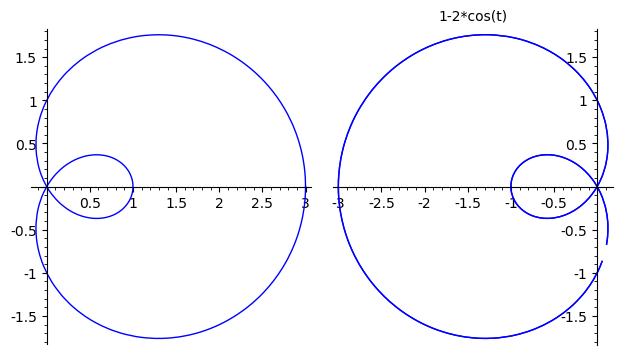
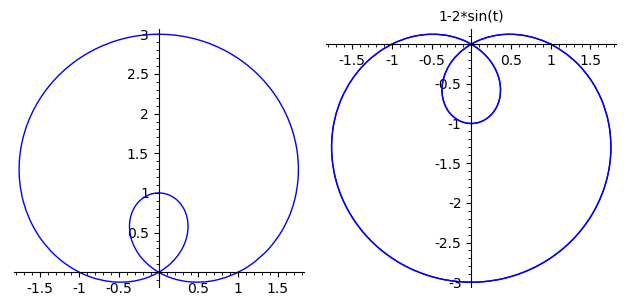
กรณี $ 0 < a < b $ จะได้ กราฟของเส้นโค้งลีมาซอง เป็นแบบมีวงวน หรือ หัวใจมีห่วง ดังนี้
เมื่อ $a=1, b=2 $ มีกราฟดังนี้
เส้นโค้งกลีบกุหลาบ
สมการทั่วไปคือ
- $r=acos(nt)$
- $r=asin(nt)$
เมื่อ $a>0$ และ$ n $ เป็นจำนวนนับ
ถ้า $ n $ เป็นจำนวนคี่ จะได้เส้นโค้งรูปกลีบกุหลาบที่มีจำนวนกลีบทั้งหมด $n $ กลีบ
ถ้า $ n $ เป็นจำนวนคู่ จะได้เส้นโค้งรูปกลีบกุหลาบที่มีจำนวนกลีบทั้งหมด $2n $ กลีบ
เช่น
- $r=2cos(3t)$จะได้เส้นโค้งรูปกลีบกุหลาบที่มีจำนวนกลีบทั้งหมด $3 $ กลีบ
- $r=3sin(2t)$จะได้เส้นโค้งรูปกลีบกุหลาบที่มีจำนวนกลีบทั้งหมด $4 $ กลีบ
การหาแกนกลางของแต่ละกลีบ หาได้ดังนี้
- หาแกนกลางกลีบแรก โดยหาค่า $t$ที่ $0 \leq t \leq \frac{\pi}{2}$ ที่ทำให้ $cos(nt)=1$ หรือ $sin(nt)=1$
- แกนกลางถัดไปจะทำมุมเพิ่มไป $\frac{2\pi}{จำนวนกลีบ}$
ตัวอย่าง
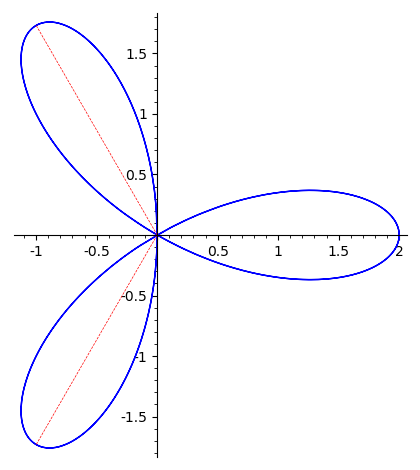
เขียนกราฟของสมการ $r=2cos(3t)$
วิธีทำ
จากสมการ $r=2cos(3t)$ มีกราฟเส้นโค้งรูปกลีบกุหลาบที่มีจำนวนกลีบทั้งหมด $3 $ กลีบ
หากลีบแรกของกราฟโดยพิจารณา $cos(3t)=1$ ได้ $t=0$
ดังนั้น แกนกลางกลีบแรกอยู่บนแกนขั้ว หรือ $t=0$
แกนกลางถัดไปจะอยู่บนเส้นตรง $0+\frac{2\pi}{3}$ และ $\frac{2\pi}{3}+\frac{2\pi}{3}=\frac{4\pi}{3}$
ดังรูป
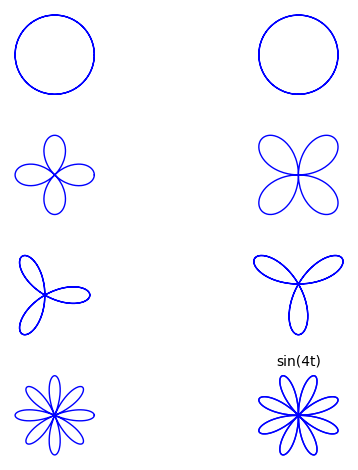
กราฟต่อไปนี้เป็นกราฟของสมการ $r=cos(nt)$ และ กราฟของสมการ $r= sin(nt)$ เมื่อ $n=1,2,3,4$
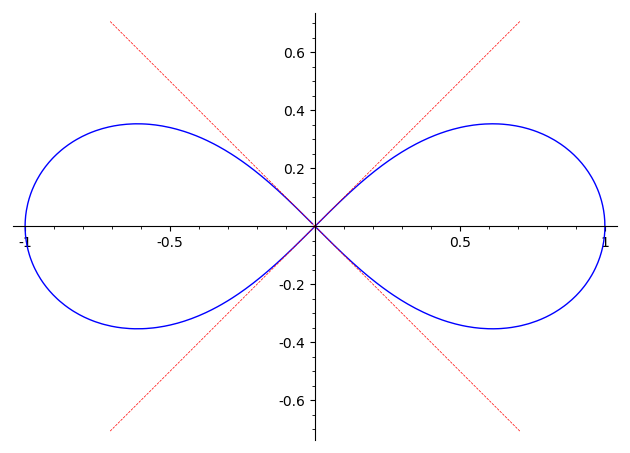
เส้นโค้งลิมนิสคต
สมการทั่วไปคือ $r^{2}= \pm a^{2}cos(2t)$ หรือ $r^{2}= \pm a^{2}sin(2t)$
เมื่อ $a > 0 $
มีกราฟเป็นรูปเลข 8 ดังนี้
ตัวอย่าง
เขียนกราฟของสมการ $r^{2}= cos(2t)$
วิธีทำ
จากสมการค่า $t$ จะต้องทำให้ $cos(2t) \geq 0$ นั่นคือ $t \in \lbrack -\frac{\pi}{4},\frac{\pi}{4} \rbrack \cup \lbrack \frac{3\pi}{4},\frac{5\pi}{4} \rbrack$
และได้กราฟดังรูป
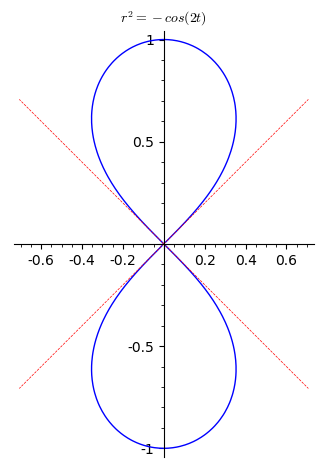
สำหรับกราฟ $r^{2}= -cos(2t)$
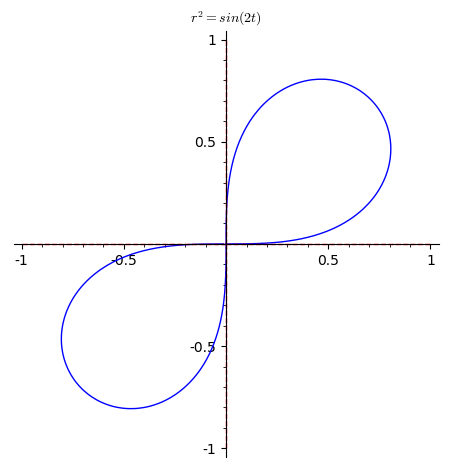
กราฟ $r^{2}= sin(2t)$
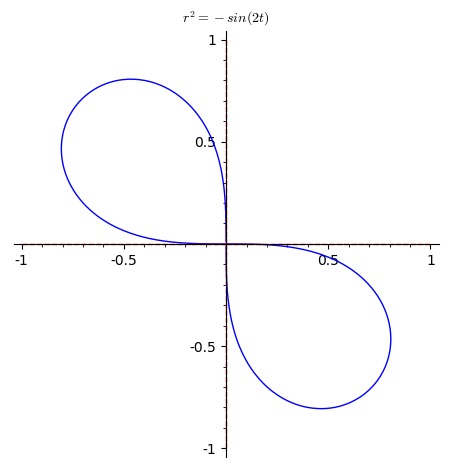
กราฟ $r^{2}= -sin(2t)$
เส้นโค้งเวียนก้นหอย
สมการทั่วไปคือ
เมื่อ $a > 0 $ มีกราฟดังนี้
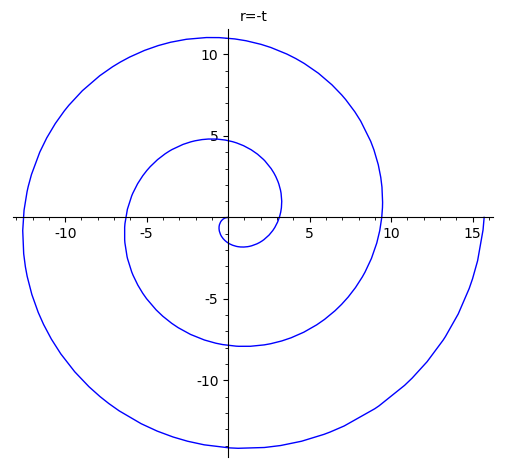
กรณีกราฟของสมการ $r=t$ เมื่อ $ 0 \leq t \leq 5\pi $
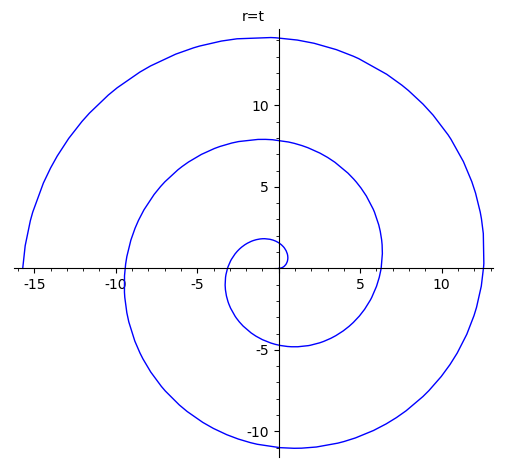
กรณีกราฟของสมการ $r=-t$ เมื่อ $ 0 \leq t \leq 5\pi $
เราสามารถใช้โปรแกรม Sage ในการวาดกราฟพิกัดเชิงขั้วได้ ดังตัวอย่างต่อไปนี้
ตัวอย่าง จงเขียนกราฟ ของ $ r=sin(2x) $
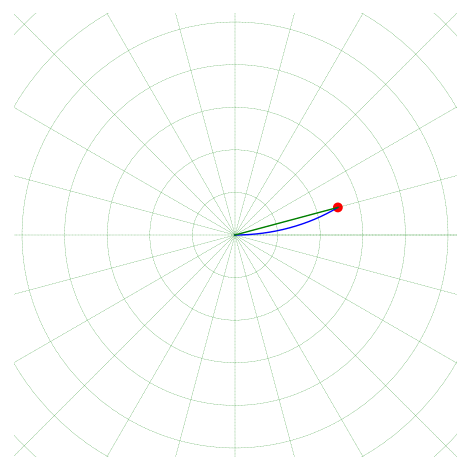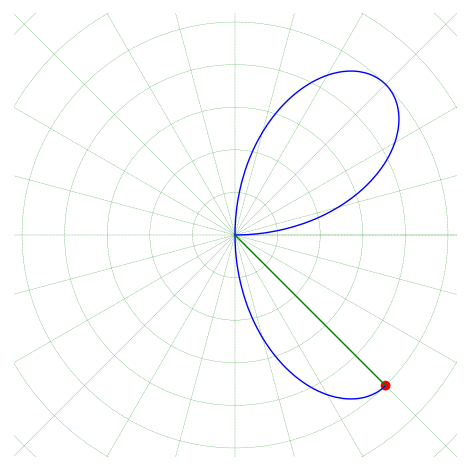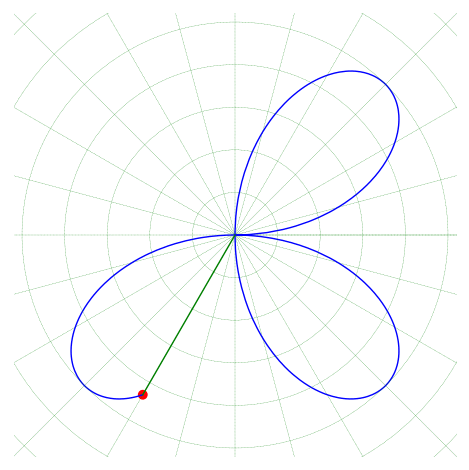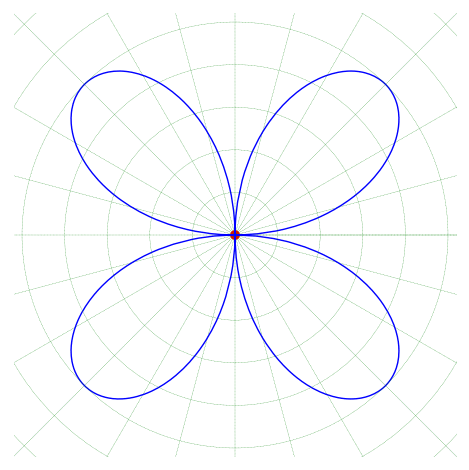
โปรแกรมSageMath
ดูทีละช่วง
การหาจุดตัดกันของกราฟในระบบพิกัดเชิงขั้ว
การหาจุดตัดกันของกราฟในระบบพิกัดเชิงขั้วมีความซับซ้อนกว่าการหาจุดตัดกันของกราฟในระบบพิกัดฉาก เนื่องจากจุดหนึ่งจุดในระบบพิกัดเชิงขั้วมีพิกัดได้หลายแบบ ไม่เหมือนในระบบพิกัดฉาก
ดังนั้น ในการหาจุดตัดของกราฟ ในระบบพิกัดเชิงขั้ว ควรพิจารณาดังนี้
- เขียนกราฟของสมการทั้งสอง
- ดูว่ากราฟผ่านจุดขั้วหรือไม่
- หาค่า $(r,t) $จากการแก้ระบบสมการของสมการทั้งสอง
- อาจจะต้องแทนค่า $(-r,\pi + t) $ ในสมการ หนึ่ง แล้วแก้ระบบสมการทั้งสอง
ตัวอย่าง
จงเขียนกราฟ $r=1+\cos t$ และ $r=1+\sin t $พร้อมหาจุดตัด ของกราฟทั้งสอง
วิธีทำ
กราฟทั้งสองสมการคือ
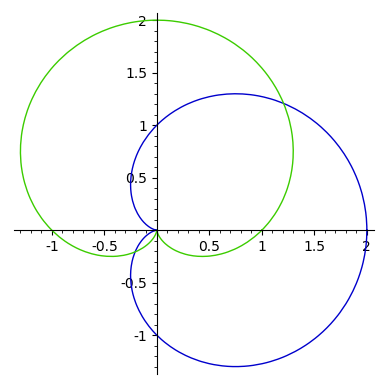
จากกราฟจะเห็นได้ว่ากราฟทั้งสองตัดกัน 3 จุด
หาจุดตัดทั้งสอง จาก ทั้งสองสมการจะได้ว่า
$$ 1+\cos t = 1+ \sin t \\
\cos t = \sin t \\
\qquad t = \frac{\pi}{4} \quad หรือ \quad \frac{5 \pi}{4}$$
ซึ่งจะเห็นได้ว่า ไม่มีจุดขั้ว แต่จากรูป จะเห็นว่า กราฟทั้งสองผ่านจุดขั้ว
ดังนั้น กราฟทั้งสองตัดกัน 3 จุดคือ
จุดขั้ว จุด $(1+\frac{\sqrt{2}}{2},\frac{\pi}{4}) $ และจุด $(1-\frac{\sqrt{2}}{2},\frac{5 \pi}{4})$
แบบฝึกหัด
จากสมการต่อไปนี้ จงเขียนกราฟในระบบพิกัดเชิงขั้ว พร้อม บอกชื่อกราฟ
$
\begin{align}
& 1.\quad r= 2+2 \sin t && 2. \quad r= 3 - 3 \cos t \\
& 3. \quad r = 6 -3 \cos t && 4. \quad r = 8+4 \sin t \\
&5. \quad r = 2- 4 \sin t && 6. \quad r= 5+10 \cos t\\
&7. \quad r = \sin 2t && 8. \quad r= \sin 3t \\
&9. \quad r = \cos 2t && 10. \quad r= \cos 3t \\
\end{align}
$
จงเขียนกราฟ พร้อมหาจุดตัดกันของกราฟทั้งสอง ดังต่อไปนี้
$
\begin{align}
11. r= 1+\sin t \quad กับ \quad r = 1-\sin t \\
12. r= 2+\sin t \quad กับ \quad r = 1-\cos t \\
13. r= 3 \cos t \quad กับ \quad r = 1-\cos t \\
\end{align}
$
การหาพื้นที่บริเวณที่ล้อมรอบด้วยเส้นโค้งในระบบพิกัดเชิงขั้ว
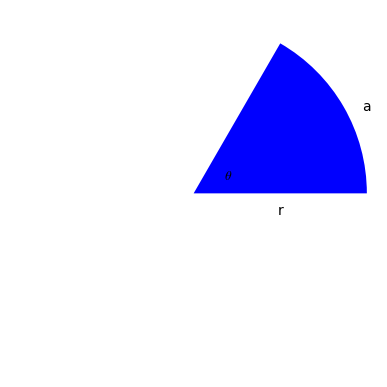
จากพื้นที่ของเซกเตอร์ของวงกลมซึ่งมีรัศมี $r$ หน่วย
ที่รองรับความยาวส่วนโค้ง $ a $ หน่วย
ซึ่งมีมุมที่จุดศูนย์กลาง $\theta $
จะได้
พื้นที่ $$A = \frac{1}{2} a r =\frac{1}{2} r^2 \theta $$
ดังรูป
ดังนั้นในการหาพื้นที่บริเวณที่ล้อมรอบด้วยเส้นโค้ง $r=f(\theta) $ เมื่อ $\theta $ อยู่ในช่วง $ [ \alpha , \beta ] $
โดยที่ $r=f(\theta) \geq 0 $ ในช่วง $ [ \alpha , \beta ] $
สามารถหาได้โดยแบ่งพื้นที่ออกเป็นพื้นที่เซกเตอร์เล็กๆจากนั้นประมาณพื้นที่ด้วยพื้นที่เซกเตอร์ของวงกลม แล้วหาค่าลิมิตเมื่อ $n \to \infty $
ซึ่งจะมีค่าเท่ากับปริพันธ์จำกัดเขต
$$A = \frac{1}{2} \int_{\alpha }^{\beta } r^2 d \theta = \frac{1}{2} \int_{\alpha }^{\beta } [f(\theta)]^2 d \theta $$
ดังทฤษฎีบทต่อไปนี้
ทฤษฎีบท
ให้ $r=f(\theta) $ เป็นเส้นโค้งในระบบพิกัดเชิงขั้ว โดยที่ $f$ เป็นฟังก์ชันต่อเนื่อง และ $f(\theta) \geq 0 $ บนช่วงปิด $ [ \alpha , \beta ] $
แล้วพื้นที่บริเวณที่ปิดล้อมด้วยเส้นโค้ง $r=f(\theta) $ และเส้นตรง $ \theta = \alpha และ \theta = \beta$
จะเท่ากับ
$$A = \frac{1}{2} \int_{\alpha }^{\beta } r^2 d \theta = \frac{1}{2} \int_{\alpha }^{\beta } [f(\theta)]^2 d \theta $$
ตัวอย่าง
จากเส้นโค้งกลีบกุหลาบ $r= \sin 2 \theta $ จงหาพื้นที่ของกลีบกุหลาบ 1 กลีบ
วิธีทำ
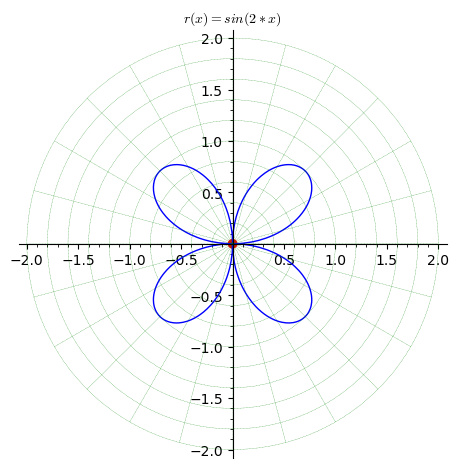
พิจารณากลีบ 1 กลีบ ของสมการ $r= \sin 2 \theta $ เมื่อ $\theta \in [0,\frac{\pi}{2} ] $
ดังนั้น พื้นที่ กลีบ 1 กลีบคือ $$A = \frac{1}{2} \int_0^{\frac{\pi}{2} } r^2 d \theta \\
= \frac{1}{2} \int_0^{\frac{\pi}{2} } ( \sin 2 \theta )^2 d \theta \\
= \frac{1}{2} \int_0^{\frac{\pi}{2} } \frac{1- \cos 4 \theta }{2} d \theta \\
= \frac{1}{4} \lgroup \theta - \frac{\sin 4 \theta }{4} \rgroup \Bigg |_0^{\frac{\pi}{2}}\\
=\frac{\pi }{8}
$$
แบบฝึกหัด
1. จงหาพื้นที่ระหว่างเส้นโค้ง $r=\sqrt{3} \cos \theta $ และ $r= \sin \theta$
2. จงหาพื้นที่ระหว่างเส้นโค้ง $r=3 \sin \theta $ และ $r= 1+ \sin \theta $
3. จงหาพื้นที่ระหว่างเส้นโค้ง $r=3 +2 \cos \theta $ และ $r=3 +2 \sin \theta $
4. จงหาพื้นที่ที่อยู่ภายใน $r=2 + \sin \theta $ แต่อยู่ภายนอก $r=3 \sin \theta $
5. จงหาพื้นที่ที่อยู่ภายใน $r=3 \sin \theta $ แต่อยู่ภายนอก $r= 2 - \sin \theta $





















